Todos los ángulos (en azul) del arco AB son iguales.
Arco capaz es el lugar geométrico de los puntos del plano desde los que se ve un segmento bajo un ángulo dado.
Dado AB, se coloca el ángulo dado, p.ej. 30º, bajo el segmento. Se hace una perpendicular p a r (base del ángulo). Trazamos la mediatriz m a AB y en el punto de intersección O con p hacemos una circunferencia de radio OA. Desde cualquier punto del arco AB por encima del segmento, por ejemplo desde C, se ve el segmento bajo un mismo ángulo (30º en este caso). Por debajo se vería bajo 180 º menos el ángulo dado, esto es 180-30=150º.
El ángulo ACB por ser inscrito es igual a la mitad del arco AB (AOB), como también lo es por ser semi-inscrito r-AB, de ahí que ACB=r-AB.

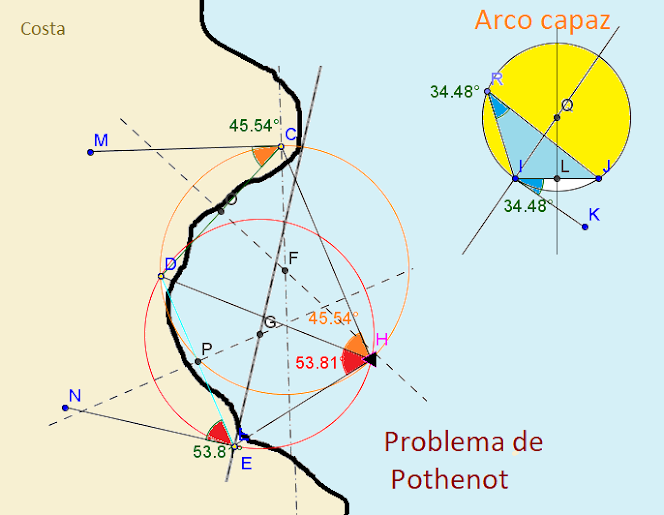
Problema de Pothenot
A la derecha vemos el procedimiento para construir un arco capaz, si sobre el segmento IJ construimos el ángulo de 34,48º y a continuación por el punto I hacemos una perpendicular a la línea que corresponde a ese ángulo, obtenemos en la intersección con la mediatriz LQ el centro Q de la circunferencia amarilla de manera que todos los triángulos cuyos vértices pasan por esa circunferencia por encima del segmento IJ tienen todos un ángulo de 34,48º, tal y como se ve por ejemplo en el punto R.
Si aplicamos esto haciendo dos arcos capaces al problema que nos ocupa podremos localizar nuestra posición exacta en el mar, siempre y cuando tengamos un plano en el que hacer los dibujos de los dos arcos capaces.
El procedimiento es el siguiente: estamos en el mar y no sabemos nuestra localización exacta pero tenemos un mapa en la que podemos ver tres puntos que pueden marcar distintas ciudades, los puntos CDE, puede ser también puntos que definen un monte característico, o un faro o cualquier otro elemento del paisaje reconocible desde nuestra posición en el barco.
Marcamos en el mapa esos tres puntos CDE y realizamos el arco capaz de los dos segmentos que definen los tres puntos.
Tenemos entonces el arco capaz del segmento DE y además el arco capaz del segmento DC. En el mapa podemos observar que, después de medir el ángulo bajo nuestro punto de vista que abarca la longitud DE, y marcar ese ángulo debajo del segmento que en este caso es 53,8º, podemos hacer la mediatriz del segmento DE y donde esa mediatriz corta a la perpendicular al segmento NE que define el ángulo 53,8 por el punto E, obtenemos el centro G de la circunferencia desde cuyos puntos se ve el segmento bajo ese ángulo.
Efectivamente todos los puntos los observamos bajo el ángulo 53.8º en la circunferencia roja y a la derecha del segmento DE.
Si hacemos el mismo proceso con el segmento DC podemos observar que bajo cualquier punto a la derecha de ese segmento sobre la circunferencia lo observamos bajo el ángulo de 45,54º.
En consecuencia la intersección de las dos circunferencias localiza la posición exacta del punto H desde el que se ven los dos segmentos bajo esos dos ángulos, de esta manera hemos podido localizar nuestra posición gracias al mapa y a una medición experimental de los ángulos vistos desde nuestra embarcación y bajo nuestro punto de vista.
Vídeo explicativo:
En el dibujo 2 vemos una aplicación de el arco capaz.